|
Zeeman effect solved
By Tejman’s
United Nature-Wave theory.
Tejman
Chaim Henry. Jerusalem.
United Nature
Theory-Wave Theory
Zeeman effect
belong to the most important scientific works
Zeeman effect = the virtual behavior of most
connections in the NATURE.
Zeeman effect named after the Dutch
physicist Pieter Zeeman, is the effect of splitting a spectral
line into several components in the presence of a static magnetic
field. It is analogous to the Stark
effect, the splitting of a spectral line into several components in the
presence of an electric field. Also similarly to the Stark
effect, transitions between different components have, in general, different
intensities, with some being entirely forbidden (in the dipole
approximation), as governed by the selection
rules.
Since the distance between the Zeeman sub-levels is a
function of the magnetic field, this effect can be used to measure the
magnetic field, e.g. that of the Sun and other stars or in laboratory plasmas.
The Zeeman effect is very important in applications such as nuclear magnetic resonance
spectroscopy, electron spin resonance spectroscopy, magnetic resonance imaging (MRI) and Mössbauer spectroscopy. It may
also be utilized to improve accuracy in atomic absorption spectroscopy. A
theory about the magnetic sense of birds assumes that a protein in
the retina is changed due to the Zeeman effect.[1]
When the spectral lines are absorption lines, the effect is called inverse
Zeeman effect.
|

|
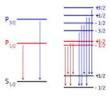
In the presence of an external magnetic field, the
weak-field Zeeman effect splits the 1S1/2 and 2P1/2
states into 2 levels each (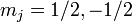 ) and the 2P3/2
state into 4 levels ( ) and the 2P3/2
state into 4 levels (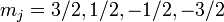 ). The
Landé g-factors for the three levels are: ). The
Landé g-factors for the three levels are: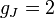 for for 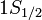 (j=1/2, l=0) (j=1/2, l=0) 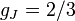 for for 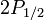 (j=1/2,
l=1) (j=1/2,
l=1) 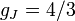 for for 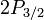 (j=3/2, l=1). Note in
particular that the size of the energy splitting is different for the
different orbitals, because the gJ values are different. On the
left, fine structure splitting is depicted. This splitting occurs even in the
absence of a magnetic field, as it is due to spin-orbit coupling. Depicted on
the right is the additional Zeeman splitting, which occurs in the presence of
magnetic fields. (j=3/2, l=1). Note in
particular that the size of the energy splitting is different for the
different orbitals, because the gJ values are different. On the
left, fine structure splitting is depicted. This splitting occurs even in the
absence of a magnetic field, as it is due to spin-orbit coupling. Depicted on
the right is the additional Zeeman splitting, which occurs in the presence of
magnetic fields.
Theoretical presentation
The total Hamiltonian of an atom in a
magnetic field is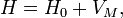 where where 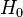 is
the unperturbed Hamiltonian of the atom, and is
the unperturbed Hamiltonian of the atom, and 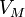 is perturbation due
to the magnetic field: is perturbation due
to the magnetic field: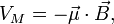 where where
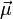 is the magnetic moment of the atom. The magnetic moment
consists of the electronic and nuclear parts; however, the latter is many
orders of magnitude smaller and will be neglected here. Therefore, is the magnetic moment of the atom. The magnetic moment
consists of the electronic and nuclear parts; however, the latter is many
orders of magnitude smaller and will be neglected here. Therefore, where where  is the Bohr
magneton, is the Bohr
magneton,  is the total electronic angular
momentum, and is the total electronic angular
momentum, and 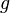 is the Landé
g-factor. The operator of the magnetic moment of an electron is a sum of
the contributions of the orbital angular momentum is the Landé
g-factor. The operator of the magnetic moment of an electron is a sum of
the contributions of the orbital angular momentum 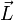 and the spin angular momentum and the spin angular momentum 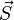 , with
each multiplied by the appropriate gyromagnetic ratio: , with
each multiplied by the appropriate gyromagnetic ratio: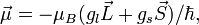 where where 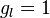 and and
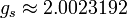 (the latter is called the anomalous gyromagnetic ratio;
the deviation of the value from 2 is due to Quantum Electrodynamics effects). In the
case of the LS coupling, one can sum over all electrons in the
atom: (the latter is called the anomalous gyromagnetic ratio;
the deviation of the value from 2 is due to Quantum Electrodynamics effects). In the
case of the LS coupling, one can sum over all electrons in the
atom: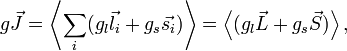 where where
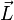 and and 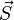 are the total orbital
momentum and spin of the atom, and averaging is done over a state with a
given value of the total angular
momentum. If the interaction term are the total orbital
momentum and spin of the atom, and averaging is done over a state with a
given value of the total angular
momentum. If the interaction term 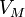 is
small (less than the fine structure), it can be treated as a
perturbation; this is the Zeeman effect proper. In the Paschen-Back effect,
described below, is
small (less than the fine structure), it can be treated as a
perturbation; this is the Zeeman effect proper. In the Paschen-Back effect,
described below, 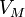 exceeds the LS
coupling significantly (but is still small compared to exceeds the LS
coupling significantly (but is still small compared to 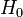 ). In
ultrastrong magnetic fields, the magnetic-field interaction may exceed ). In
ultrastrong magnetic fields, the magnetic-field interaction may exceed 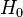 ,
in which case the atom can no longer exist in its normal meaning, and one
talks about ,
in which case the atom can no longer exist in its normal meaning, and one
talks about
|
|

|
|
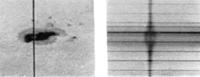
Zeeman effect on a sunspot spectral line
|
Solar magnetogram
|
Breit-Rabi solution formula we will include the hyperfine structure (interaction between the
electron's spin and the magnetic moment of the nucleus), which is governed by
the quantum number 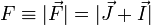 , where , where 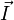 is the spin
angular momentum operator of the nucleus. Alternatively, the derivation could
be done with is the spin
angular momentum operator of the nucleus. Alternatively, the derivation could
be done with 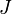 only. The constant only. The constant 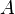 is known as the
zero field hyperfine constant and is given in units of Hertz. is known as the
zero field hyperfine constant and is given in units of Hertz. 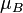 is the Bohr
magneton. is the Bohr
magneton. 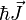 and and 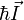 are
the electron and nuclear angular momentum operators. are
the electron and nuclear angular momentum operators. 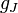 and and 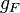 can be
found via a classical vector coupling model or a more detailed quantum
mechanical calculation to be: As
discussed, in the case of weak magnetic fields, the Zeeman interaction can be
treated as a perturbation to the can be
found via a classical vector coupling model or a more detailed quantum
mechanical calculation to be: As
discussed, in the case of weak magnetic fields, the Zeeman interaction can be
treated as a perturbation to the 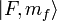 basis. In the high
field regime, the magnetic field becomes so large that the Zeeman effect will
dominate, and we must use a more complete basis of basis. In the high
field regime, the magnetic field becomes so large that the Zeeman effect will
dominate, and we must use a more complete basis of 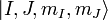 or
just or
just 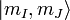 since since 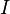 and and 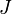 will be constant within
a given level. will be constant within
a given level.
To get the complete picture, including intermediate field
strengths, we must consider eigenstates which are superpositions of the 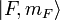 and and 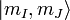 basis states.
For basis states.
For 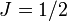 , the Hamiltonian can be solved analytically, resulting in the
Breit-Rabi formula. Notably, the electric quadrapole interaction is zero for , the Hamiltonian can be solved analytically, resulting in the
Breit-Rabi formula. Notably, the electric quadrapole interaction is zero for 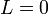 ( (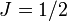 ),
so this formula is fairly accurate. ),
so this formula is fairly accurate.
To solve this system, we note that at all times, the total
angular momentum projection 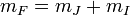 will be conserved.
Furthermore, since will be conserved.
Furthermore, since 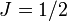 between states between states 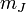 will
change between only will
change between only 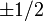 . Therefore, we can define
a good basis as: . Therefore, we can define
a good basis as: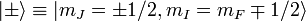 We now
utilize quantum mechanical ladder
operators, which are defined for a general angular momentum operator We now
utilize quantum mechanical ladder
operators, which are defined for a general angular momentum operator 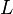 as as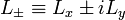 These ladder operators have the property These ladder operators have the property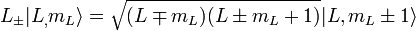 as
long as as
long as 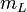 lies in the range lies in the range 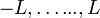 (otherwise,
they return zero). Using ladder operators (otherwise,
they return zero). Using ladder operators 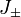 and and 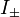 We can
rewrite the Hamiltonian as We can
rewrite the Hamiltonian as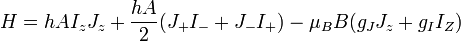 Now we can determine the matrix elements of the Hamiltonian:
Now we can determine the matrix elements of the Hamiltonian: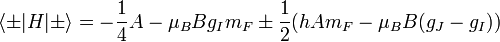 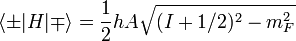 Solving
for the eigenvalues of this matrix, (as can be done by hand, or more easily,
with a computer algebra system) we rrive at the energy shifts: Solving
for the eigenvalues of this matrix, (as can be done by hand, or more easily,
with a computer algebra system) we rrive at the energy shifts: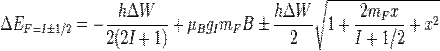
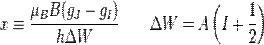 where where
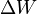 is the splitting (in units of Hz) between two hyperfine
sublevels in the absence of magnetic field is the splitting (in units of Hz) between two hyperfine
sublevels in the absence of magnetic field 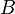 , ,
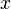 is referred to as the 'field
strength parameter' (Note: for is referred to as the 'field
strength parameter' (Note: for 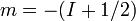 the square root is an
exact square, and should be interpreted as the square root is an
exact square, and should be interpreted as 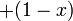 ). This equation is known
as the Breit-Rabi formula and is useful for systems with one valence
electron in an ). This equation is known
as the Breit-Rabi formula and is useful for systems with one valence
electron in an  ( (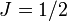 ) level.[3][4] ) level.[3][4]
Note that index 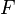 in in 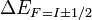 should
be considered not as total angular momentum of the atom but as asymptotic
total angular momentum. It is equal to total angular momentum only if should
be considered not as total angular momentum of the atom but as asymptotic
total angular momentum. It is equal to total angular momentum only if 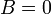 otherwise
eigenvectors corresponding different eigenvalues of the Hamiltonian are the
superpositions of states with different otherwise
eigenvectors corresponding different eigenvalues of the Hamiltonian are the
superpositions of states with different 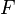 but equal but equal 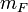 (the only exceptions
are (the only exceptions
are 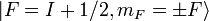 ). ).
http://en.wikipedia.org/wiki/Zeeman_effect
Zeeman
Effect in Hydrogen
When an external magnetic field is applied, sharp spectral
lines like the n=3→ 2 transition of
hydrogen split into multiple closely spaced lines. First observed by
Pieter Zeeman, this splitting is attributed to the interaction between the
magnetic field and the magnetic
dipole moment associated with the orbital
angular momentum. In the absence of the magnetic field, the hydrogen
energies depend only upon the principal
quantum number n, and the emissions occur at a single wavelength.
Note that the transitions shown follow the selection
rule which does not allow a change of more than one unit in the quantum
number
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/zeeman.html
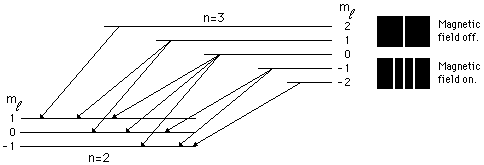
The pattern and amount of splitting are a
signature that a magnetic field is present, and of its strength. The
splitting is associated with what is called the orbital angular momentum
quantum number L of the atomic level. This quantum number can take
non-negative integer values. The number of split levels in the magnetic field
is 2 * L + 1. The following figure illustrates the Zeeman effect.
|
|
|
The Zeeman Effect
|
Atomic physicists use the
abbreviation "s" for a level with L=0, "p" for L=1, and
"d" for L=2, and so on (the reasons for these designations are of
historical interest only). It is also common to precede this designation with
the integer principle quantum number n. Thus, the designation "2p"
means a level that has n=2 and L=1. In the preceding example the lowest level
is an "s" level, so it has L=0 and 2L + 1 = 1, so it isn't split in
the magnetic field, while the first excited state has L=1 ("p"
level), so it is split into 2L + 1 = 3 levels by the magnetic field. Thus, a
single transition is split into 3 transitions by the magnetic field in this
example. The Zeeman effect can be interpreted in
terms of the precession of the orbital angular momentum vector in the
magnetic field, similar to the precession of the axis of a spinning top in a
gravitational field.http://csep10.phys.utk.edu/astr162/lect/light/zeeman-split.html
For better understanding Zeeman effect cxxsee Electron
motion, spin, waltz solution-Tejman.
This swirling
rotation and revolving motion of electric strong force path create two semi
loops quantum formations.
|
 Black hole or energetic source expell.energetic pathr
moving by curvatures and by dint of its Black hole or energetic source expell.energetic pathr
moving by curvatures and by dint of its
|
|

|
|
swirling and spinning space time behaviors create open continue
quanta formations and. exactly like known retrograde motion.
|
Wave formation: (quantum).The energetic loop to the right (of both
pictures) pushes outward, while the magnetic-gravity loop (left) pushes the
energetic matter inside.
|
Every stable
{quantum} formation must have two behaviors: Electric {strong force}
semi-loop and gravity-magnetic {weak force} of 6 quarks [+ +and -] and
gravity semi loop [- - and+] which must be in equilibrium in all phase
transitions. See Tejman phase transitions
For
understanding quantum endless formations please see some examples
Different quanta formations
Example: Two
semi loops- by strong force- closed quanta formations
Picture, GALAXY
M-51 closed quantum formation.
|

Stefan's Quintet. 7317-
 merging galaxy[quantum] merging galaxy[quantum]
|

NASA M-51 The magnetic swirl, to the right, and the
energetic swirl, left- together quantum- gravitational wave
formation.
|
Independent
closed
quantum formation
connected
by energe-
tic paths They are not
collisions
galaxies
|
Two semi loops of the one
quantum formation connected by path.
|
Electric part of M-51 + lt
|
Gravity
magnetic part M-51-rt
|
Other connections
Two Semi loops open quanta formations by continue
energetic path.
|

|
|
|
Motion of energetic
matter
From Hubbell
Telescope.
|
Motion of energetic
matter in DNA
|
Other type of quanta closed gravity semi loop
quantum.
Gravity super
nova, earth, sun, electron [two electrons virtual molecule], neutrino living
creation,. molecules. electron galaxies, universes they are
stabile
formations that means that they are quanta two forces and Tejman’s article
“Electron motion spin explained the NATURE ingenious creation.
in
closed gravity semi loop electron on basis NATURE observations and conclusion.
1 Aurora earth prominence.
Gravity semi loops quantum
2 From electric swirl continue energetic path which by swirling
motion create second swirl [like white hole-Schwarzschild swirl]
3 Schwarzschild swirl by retrograde motion create gravity paths
4 Gravity path by peculiar motion move to ‘”south pole” and create
create like ‘black hole” which create again electric path to
continue motion of energetic matter in closed gravity semi loop and bubble
[electron\.
Coriolis forces are forces of
closed quantum formation
(1)(2)(3) The
motion of Coriolis force (Energetic matter motion) (4)(5)(6) Coriolis
Force – the force is the same however it has two different representations at
the northern and southern parts of the earth, hence the different
Gravity
path from North Pole [-] to South Pole and electric paths [+] from South Pole
to North direction.
Pict.
From Neutron stars by Steve Nadis [astronomy
march 1999] p.52.
Expelled energetic path from energetic creation create quanta
formations,
Circulation of energetic matter in electron,
bubble and closed quantum formation.
1 Electric
swirl [Kerr, black hole]
2 Expelled
electric path [with clockwise rotation Coriolis forces]
3 Creates
white hole swirl [Schwarzschild swirl]
4 Schwarzschild
swirl creates magnetic path [Coriolis contra clockwise forces]
5 Those
forces move from north to south
6 Create
closed energetic circulation in electron [closed gravity quantum formation]
That means
electron, earth are closed quanta formations.
Virtual quanta not connected by energetic path only
by virtual wave forces.
The quanta behavior is endless so appears different
quanta formations and equations [but
always with balance of both forces semi ].
|
Schrödinger’s
equation:
|
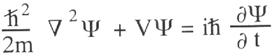
|
|
Faraday’s
equation:
|
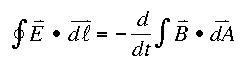
|
|
Maxwell equation:
|
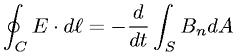
|
|
Planck’s
equation:
|
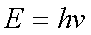
|
|
Einstein’s
equation:
|
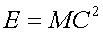
|
The de Broglie
equation f =E/h,
or E= fXh
Tejman’s equation claims:
that for stabile quantum formation must always be energetic equilibrium of
[two semi loops] bubbles forces.
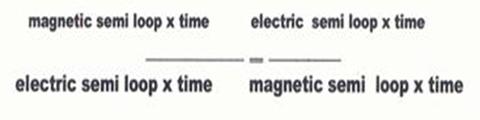
This mixed electromagnetic force [two semi loops
bubbles] appears in superposition [of two bubbles behaviors] as one entity
like Schrödinger’s cat paradox.
The ideal structure of energetic matter is the wave formation,
which is comprised of an energetic and magnetic loop. Under ideal conditions,
such as the photon, the two loops are equal insofar as the properties of
their energetic matter are concerned.
The structure of the wave formation is amenable to the
creation of various life forms. Any change in the proportion of energetic
matter in the loops leads to a new phase transition in which one of the loops
has more energetic properties. These changes to the equilibrium between the
energetic and magnetic loop result in different behaviors.
To follow are mathematical equations for the balance between
the energetic and magnetic loop of a wave formation in various phase
transitions:
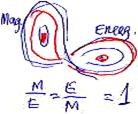
1. High Energetic Phase Transition (Hyperspace):
|
Energetic Loop(x)
|
=
|
Magnetic Loop
|
= 1 = 1
|
Energetic Loop(x) 
|
|
Magnetic Loop
|
Energetic Loop(x)
|
Magnetic Loop 
|
In hyperspace, energetic matter (energy, space and time) propagates
endlessly, while the magnetic loop (matter) almost disappears. 
2. The Duality
Phase:
|
Energetic Loop
|
=
|
Magnetic Loop
|
= 1 = 1
|
|
|
Magnetic Loop
|
Energetic Loop
|
|
The phase transition of a photon is in a state of duality whereby the
magnetic loop equals the energetic loop, which equals 1. In this phase, both
loops are balanced and therefore the photon has the longest lifespan.
3. Low
Energetic-High Magnetic Phase Transition
|
Magnetic Loop(x)
|
=
|
Energetic Loop
|
= 1 = 1
|
Energetic Loop(x) 
|
|
Energetic Loop
|
Magnetic Loop(x)
|
Magnetic Loop 
|
|
In this phase,
the magnetic loop is induced to compliment the energetic loop by
accelerating the pace at which it spins. This helps maintain the
equilibrium of the wave. Moreover, energy, space, and time are most
condensed in this phase, as the magnetic properties (loop) gain the
ascendancy! In fact, this is exactly what transpires in a nuclear bomb, as
extremely condensed units of energy, space and time are released by the
explosion.
Every quantum
formation transferee from high energetic level [phase] to lower energetic
level by dispersing energetic matter.
Two like
electrons, atoms or molecules create virtual quantum [not connected by
strong foces. The one electron became electric
properties and second gravity spin like atoms molecules and isomers
formations and easy separate [Quantum formation by energetic path very
difficult to split] . 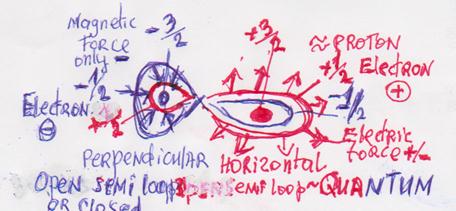
|
|
|
Electron -
|
Virtual weak
connection
|
Electron +
|
|
|
Quarks d d u
|
Quarks u u d
|
|
|
|
|
|
|
Very simple explanation of quantum structure and
behavior of virtual quantum of 2 electrons not connected by strong force only
by virtual energetic path This virtual connection is the most ingenious
sophisticated of NATURE creation of endless different creations mainly of
living formation.
This picture explained electrons e+ and electron e-
behavior and Zeeman effect 1 2 3. and 1 2 3 quarks lines
|
csep10.phys.utk.ed
The Zeeman Effect
|
 en.wikipedia.org en.wikipedia.org
Zeeman effect - Wikipedia
|
 en.wikipedia.org en.wikipedia.org
inverse Zeeman effect.
|
 faculty.gvsu.edu faculty.gvsu.edu
as the Zeeman effect.
|
In all quanta equations, energetic matter-forces are
in superposition,
That means that electron ruled by two forces in
gravity phase transition. Electron
the most condensed wave formation creates closed wave particle, closed
quantum formation [example chicken eggs see gravity semi loop.
All quanta equations are viable also to electron
closed quantum in gravity phase transition
Summary
Zeeman
effect = the
virtual forces behavior are the most connections in NATURE including living
creations.
|

|
Yours waves
quanta frequency are very nice, adorable.
|

|

|
Yours
waves quanta frequency are pfu, , pfu
|
This paper may
be subject to copy, but please cited the source.
© Copyright:
Dr. Tejman Chaim, Henry. Decmber 2012
Theory of
everything. http://www.grandunifiedtheory.org.il/
Copy send to NATURE
journal.
|